The graph of the equation y = ax2 bx c is a parabola congruent to the graph of y = ax2 Recall that a quadratic function is any function f whose equation can be put in the form f(x) = ax2 bx c, where a ≠ 0 Thus, the graph of every quadratic function is a parabola, with y–intercept f(0) = cFree Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation HistoryMathy=x^2bxc/math What we are really looking for is a value for mathb/math and mathc/math Once we can find those two values, we can simply plug them back into mathy=x^2bxc/math to get the equation of the parabola Let's start

The Tangent To Y Ax 2 Bx C At 1 2 Is Parallel To The Normal At The Point 2 2 On The Youtube
Y=ax^2+bx+c solve for c
Y=ax^2+bx+c solve for c-Y= ax^2 bx c = (4 3^05)*x^2 (4 2* (3^05))*x 4 b) y= ax^2 bx c has vertex (4,1) and passes through (1,11) 1 = 16a 4b c 11 = a b c the vertex is x = b/2a that is b/2a = 4 by solving the system of equations 16a 4b c = 1 a b c = 11 b/2a = 4Answer the parabola y = ax2 bxc doesn't intersect the xaxis We can write a better program to deal




alog Transform Quadratic Function Y Ax2 Bx C 0 Into Vertex Form Y A X H 2 K Youtube
What is the equation of the axis of symmetry of the graph of y=ax^2bxc 2 See answers calculista calculista Answer Stepbystep explanation we know that The quadratic equation is a vertical parabola The axis of symmetry in a vertical parabola is a vertical lineWhat does 'nan' mean? Synthetic division by a x 2 b x c I know that synthetic division can be used in order to find quotient q ( x) and remainder r ( x) of a polynomial p ( x) when it is divided by some linear polynomial like x − c Now, does exist some procedure (another than long division) in order to find q ( x) and r ( x) when the divisor is a x 2 b x
Learn termquadratics = y = ax^2 bx c with free interactive flashcards Choose from 68 different sets of termquadratics = y = ax^2 bx c flashcards on Quizlet Secondly, how do you find the Y intercept of ax 2 bx c?Answer to Find the derivative of y(x) = ax^2bxc By signing up, you'll get thousands of stepbystep solutions to your homework questions You
Parabola Equation The standard equation of a parabola is given by {eq}y=ax^2bxc {/eq} where a and b are constants, and c is a constant representing the yinterceptRewrite the equation as ax2 bx c = y a x 2 b x c = y Move y y to the left side of the equation by subtracting it from both sides Use the quadratic formula to find the solutions Substitute the values a = a a = a, b = b b = b, and c = c−y c = c y into the quadratic formula and solve for x x Simplify the numeratorDifferentiate the function y = ax^2 bx c




The Tangent To Y Ax 2 Bx C At 1 2 Is Parallel To The Normal At The Point 2 2 On The Youtube



Assignment 2
Hi everyone, I'm facing some troubles with eliminating constants to make the differential equation from this ordinary equation y=ax^2 bx c, where a, b and c are constants I'm familiar with eliminating two constants at most like theSuppose you have ax 2 bx c = y, and you are told to plug zero in for y The corresponding xvalues are the xintercepts of the graph So solving ax 2 bx c = 0 for x means, among other things, that you are trying to find xintercepts Since there were two solutions for x 2 3x – 4 = 0, there must then be two xintercepts on the graph Graphing, we get the curve belowThe yintercept is located at the point (0, c) The solutions of the quadratic equation ax 2 bx c = 0 correspond to the roots of the function f(x) = ax 2 bx c, since they are the values of x for which f(x) = 0



Ppt Standard Form Of Quadratic Function Y Ax 2 Bx C Powerpoint Presentation Id




Regression Analysis Of The Relationship Y Ax 2 Bx C Between Download Table
Find the yintercept for the equation by letting x equal zero The equation becomes y = 0x squared 0x c or y = c Note that the yintercept of a quadratic equation written in the form y = ax squared bx = c will always be the constant c To find the xintercepts of a quadratic equation, let y = 0For example, a univariate quadratic function has the form f = a x 2 b x c, a ≠ 0 {\displaystyle f=ax^{2}bxc,\quad a\neq 0} in the single variable x The graph of a univariate quadratic function is a parabola whose axis of symmetry is parallel to the yaxis, as shown at right If the quadratic function is set equal to zero, then the result is a quadratic equation The solutions to theFor more problems and solutions visit http//wwwmathplanetcom



Quadratic Function Y Ax 2 Bx C Quadratic



Given A Parabola Having Equation Y Ax 2 Bx C With A 0 What Are The Coordinates Of The Vertex Quora
Find the derivative of y = ax^2 bx C Assume that a, b and c are constants dy/dx = Question Find the derivative of y = ax^2 bx C Assume that a, b and c are constantsSteps for Solving Linear Equation a x b x = c − a x b x = c Subtract \left (a\right)x from both sides Subtract ( − a) x from both sides bx=c\left (a\right)x b x = c − ( − a) x Multiply 1 and 1 to get 1 Multiply − 1 and − 1 to get 1Step 3 Let us again start with equation y = ax 2 bx c Let a=1, b=0, and vary c, resulting in y = ax 2 c Note that this investigation is not complete until we review the effects that variable 'b' my have with respect to variable 'c' The value of variable 'c' moves the parabola shifts up and down with respect to the yaxis




Consider The Following Formulae Y Ax2 Bx C Z 1 Gauthmath



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com
How to solve an equation y=ax^2bxc when x is unknown and y known Ask Question Asked 11 months ago Active 11 months ago Viewed 102 times 1 I have this equation y = *x^*x And I would like to obtain the result of the equation when I give "y" numbers, editedIn algebra, a quadratic equation is any polynomial equation of the second degree with the following form ax 2 bx c = 0 where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant The numerals a, b, and c are coefficients of the equation, and they represent known numbers For example, a cannot be 0, or the equation would be linearParabolas Parabolas The graph of a quadratic equation in two variables (y = ax2 bx c) is called a parabola The following graphs are two typical parabolas their xintercepts are marked by red dots, their yintercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot We say that the first parabola opens upwards (is a U shape) and the second



How To Determine A Quadratic Function Y Ax 2 Bx C If Its Graph Passes Through The Point 2 19 And It Has A Horizontal Tangent At 1 8 Quora




Estimates Of The Regression Coefficients For The Model Y Ax 2 Bx Download Table
Click here👆to get an answer to your question ️ The graph of the equation y = ax^2 bx c has shape open upwards like which is known as parabola, when Join / Login maths The graph of the equation y = a x 2 b x c has shape open upwards like which is known as parabola,If y=ax^(2)bxc is the reflection of parabola y=x^(2)4x1 about the line y=3,abc= The locus of the middle points of all chords of the parabola y^(2)=4ax passing through the vertex is y=a(x2)(x4) In the quadratic equation above, a is a nonzero constant Solve for x' and y' and plug into y'=ax'2, get (yy_0)=a(xx_0)^2, now you are back in the original systemYour b =2ax_0, where x_0 is the xcoordinate of the vertexLet me know if ok $\endgroup$ – Peter Szilas Sep 27 '18 at 1756
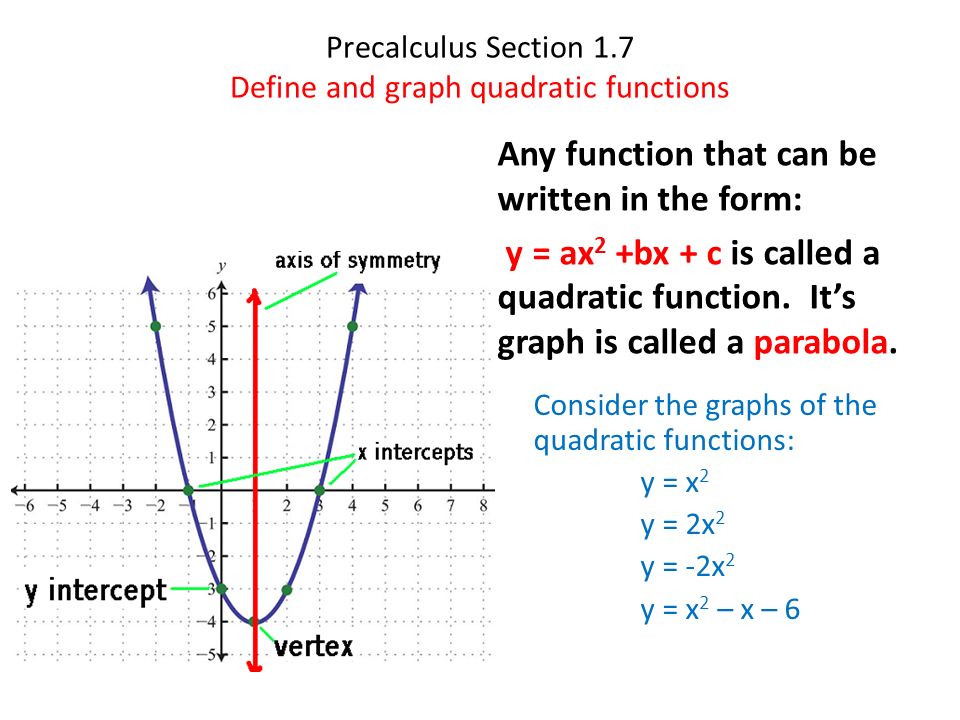



Precalculus Section 1 7 Define And Graph Quadratic Functions Any Function That Can Be Written In The Form Y Ax 2 Bx C Is Called A Quadratic Function Ppt Download




The Graph Of Y Ax 2 Bx C Is Shown Below Determine The Solution Set Of 0 Ax 2 Bx C 1 Brainly Com
STDIN a b c x1 x2 x3 and x is in sorted order ie x1 < x2 < x3 The Code should generate a new list ( y = y1 y2 y3 ) using the parabola equation for every x and sort the above list with a runtime complexity of A quadratic function is a function of the form y = ax 2 bx c, where a≠ 0, and a, b, and c are real numbers How does b affect the parabola?Given a quadratic equation y = ax^2 bx c, (i) What is the effect of changing the value of the number c on the parabola?




J 4 Y 1 0 13 Focus Of Parabola Y Ax2 Bx C Is



Graphing Quadratic Functions Y 2 Ax Bx C
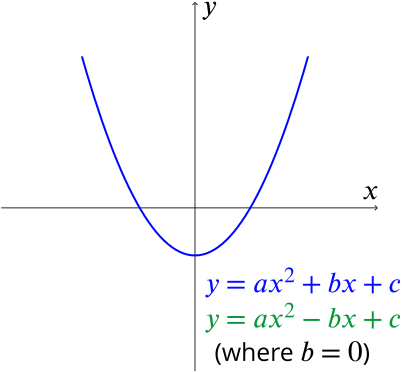
When b = 0, the vertex of the parabola lies on the yaxis Changing b does not affect the shape of the parabola (as changing a did)Answer y = ax2 bxc The vertex will correspond to the point where the curve attains a minima (a> 0) or maxima (a < 0) ∴ dxdy = 2axb = 0 ⇒ x = 2a−bThis is your generic quadratic equation y = ax 2 bx c Move the loose number over to the other side y – c = ax 2 bx Factor out whatever is multiplied on the squared term Make room on the lefthand side, and put a copy of " a " in front of this space




Y Ax2 Bx C Graph Novocom Top




In other word, if two parabolas have the same coefficients a, and b, 39,850 results, page 18 Problem 1 Formula y = ax2 bx c y = 5x2 10x – 3 Directions find the vertex, yintercept and axis of symmetry Then you may graph 10 Problem 1 Formula y = ax2 bx c y = 5x2 10x – 3 The first thing we will find is the vertex(Answer not a number) 4 What is the geometric interpretation of the discriminant being negative?




How To Complete The Square Of Quadratic Equation Of Y Ax 2 Bx C By Mthokozisi Issuu
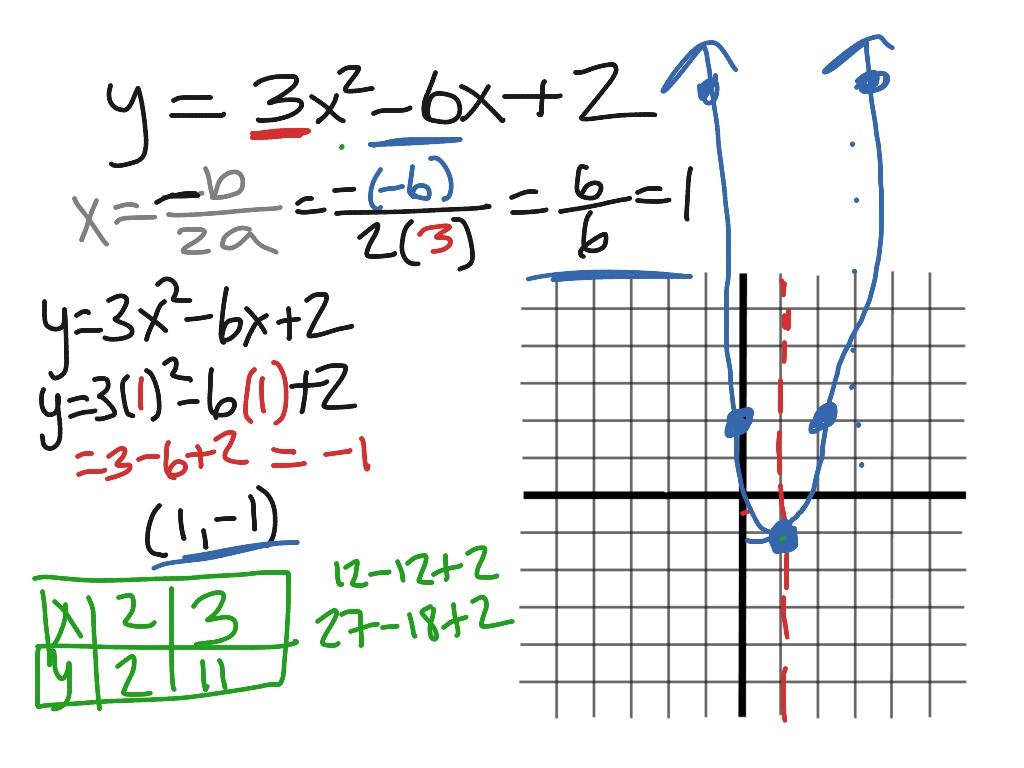



10 2 Graph Ax 2 Bx C Math Showme
5) The xcoordinate of the vertex is at b/2a The ycoordinate of this vertex is found by plugging in x = b/2a into ax^2 bx c Those aren't really handy for graphing, however What you do in practice if you want to graph ax^2 bx c is you complete the square You get itThe vertex of y = a x 2 b x c Set a = 1, b = − 4, and c = 2 to look at the graph of y = x 2 − 4 x 2 Using the formula x = − b 2 a , you can calculate that the axis of symmetry of this parabola is the line x = 2 Also, notice that the vertex of this parabola is the point ( 2, − 2) Now slide c to 45 Find the differential equation of ln y = ax^2 bx c by eliminating the arbitrary constants a, b and c Homework Equations Wrosnkian determinant The Attempt at a Solution I've solved a similar problem (y=ax^2bxc > y'''=0), but couldn't do the same with this one All what I could is taking the exponent of both sides > y=e^(ax^2 bx c)
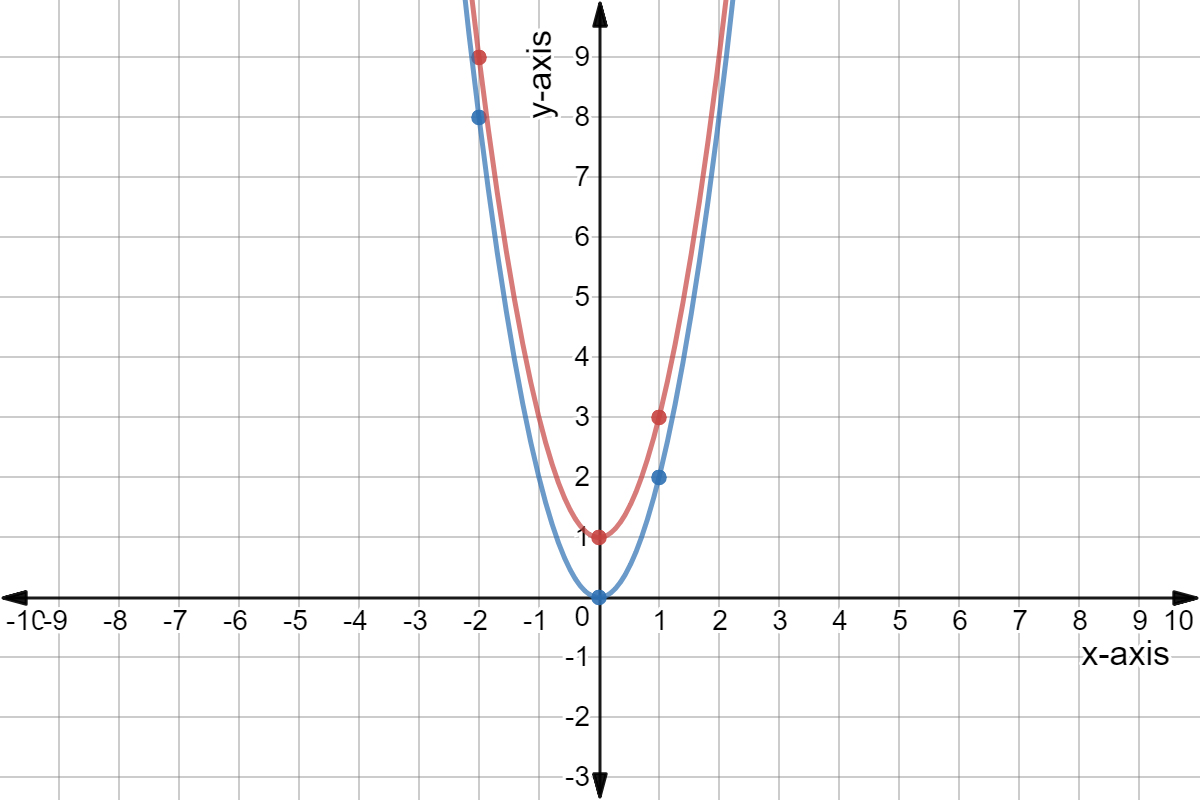



Quadratic Graph Example Y Ax C Expii



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
The quadratic equation itself is (standard form) ax^2 bx c = 0 where a is the coefficient of the x^2 term b is the coefficient of the x term c is the constant term you use the a,b,c terms in the quadratic formula to find the roots the minimum / maximum point ofLearn termquadratic form = ax^2bxc with free interactive flashcards Choose from 66 different sets of termquadratic form = ax^2bxc flashcards on Quizlet1Y=ax^2bxcSlope of the curve at x=0 equals the incoming slope at the point of vertical curve(g1)This the value of b=g view the full answer



The Graph Of Y Ax 2 Bx C Is Given In The Chegg Com



A Sketch Of Y Ax2 Bx C Is Shown B The Maximum Poi Gauthmath
When the graph of \(y = ax^2 bx c \) is drawn, the solutions to the equation are the values of the xcoordinates of the points where the graph crosses the xaxis Example #y=ax^2bxclarr" c is a constant"# #rArrdy/dx=2ax^(21)bx^(11)0# #=2ax^1bx^00=2axb# Maths The curve y = ax^2 bx c touches the line y = 2x at the origin and has a maximum point at x = 1 Find the values of a, b and c you have given equations you can derive max at x=1y"= negative=2 *da/dx which means a has to be negative for the derivative to be negative
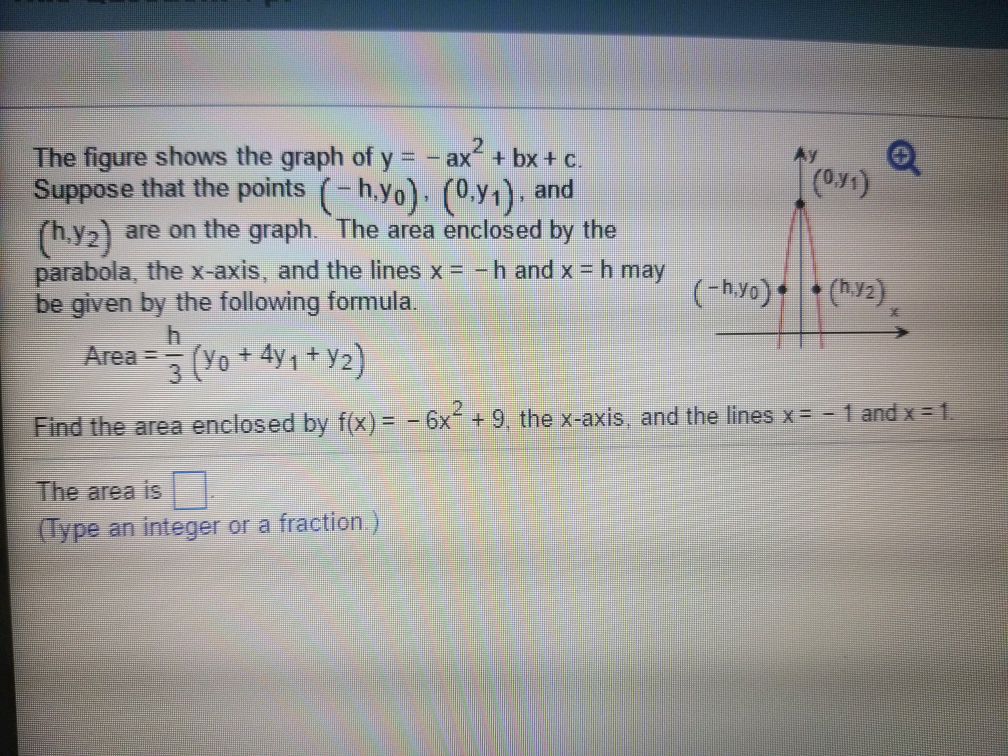



The Figure Shows The Graph Of Y Ax 2 Bx C Chegg Com




Quadratic Function Wikipedia
The equation `y=ax^2bxc` is a means of describing the quadratic function If a quadratic function is equal to zero, the result will be a quadratic equation with The parabola with equation y=ax^2bxc is graphed below 0 1154 1 The parabola with equation y=ax^2bxc is graphed below The zeros of the quadratic ax^2 bx c are at x=m and x=n, where m>n What is mn?Question 2519 A parabola y = ax^2 bx c has vertex (4, 2) If (2, 0) is on the parabola, then find the value of abc If (2, 0) is on the parabola, then find the value of abc Answer by Fombitz() ( Show Source )



Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id
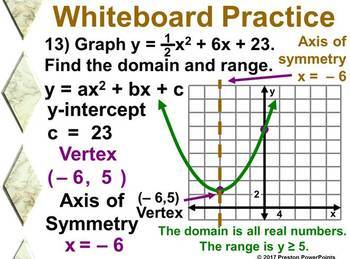



Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt
Ax^2bxc=0 x^2x6=9 x^2x6=0 x^21=0 x^22x1=3x10 2x^24x6=0 quadraticequationcalculatorBy asking about "h", it seems that you mean X coordinate of vertex(h,k) If so, Y = aX^2 bX c => Y = a(X^2 bX/a) c => Y = a(X^2 bX/a b^2/4a^2) c b^2/4a => Y = a(X b/2a)^2 (4ac b^2)/4a This equation is simplified into Y = a(X2,b = 5,c = 4?




Refer The Picture Also Y Ax 2 Bx C Hd Png Download Transparent Png Image Pngitem




The Graphs Of The Two Equations Y A X 2 B X C And Y A X 2 B X C Such That Brainly In
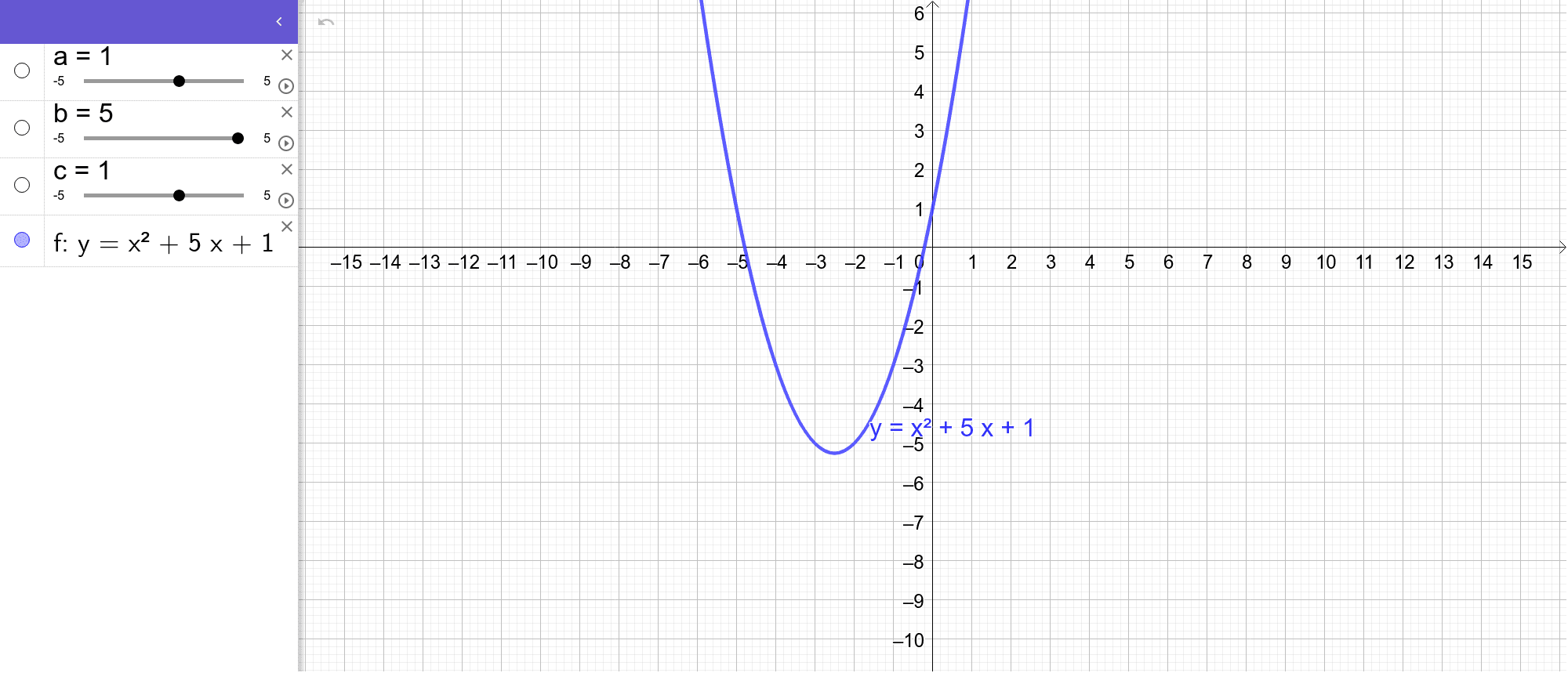



Y Ax 2 Bx C Geogebra




The Adjoining Figure Shows The Graph Of Y Ax 2 Bx C Then Youtube



Math Spoken Here About Quadratics 3



Unique Quadratic Equation In The Form Y Ax 2 Bx C



Show That Y Ax 2 Bx C A 0 Represents A Parabola And Find Its Vertex Focus Directrix And Latus Rectum Sarthaks Econnect Largest Online Education Community




Graphing Y Ax 2 Bx C




8 3 Graphing F X Ax 2 Bx C Youtube



Exploring Parabolas Y Ax 2 Bx C




Standard Form Y Ax2 Bx C Factored Form Y A X S X T




Quadratic Formula Wikipedia



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com
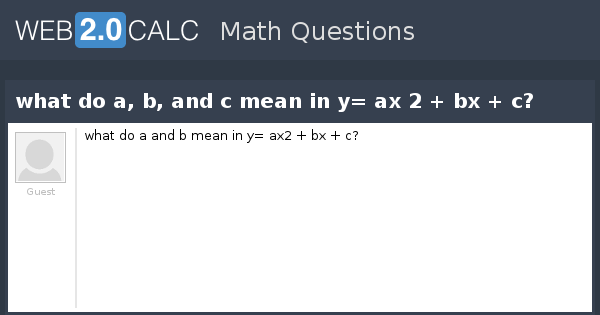



View Question What Do A B And C Mean In Y Ax 2 Bx C
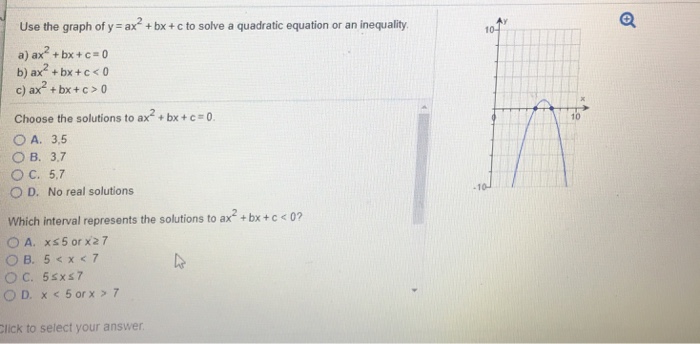



Use The Graph Of Y Ax 2 Bx C To Solve A Chegg Com



1



1
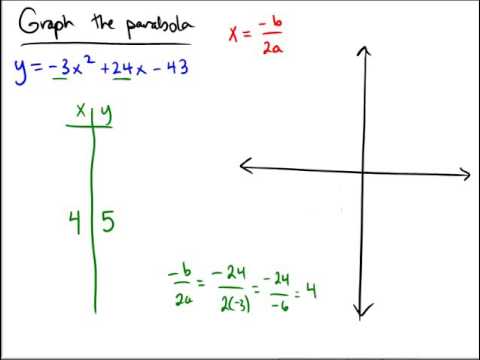



Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube




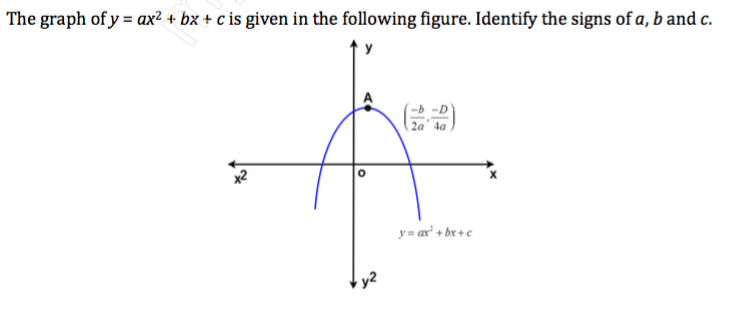
The Graphs Of Y Ax 2 Bx C Are Given In Figure Identify The Signs Of A B And C In Each Of The Following



Quadratic Function Y Ax2 Bx C When A Is Sutori




Quadratic Formula Calculator



Math Spoken Here About Quadratics 3



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




If The Curve Y Ax 2 Bx C Passes Through The Point 1 2 And The Line Y X Touches Youtube



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego




alog Transform Quadratic Function Y Ax2 Bx C 0 Into Vertex Form Y A X H 2 K Youtube




Equation Model Of Sorption Curve Y Ax 2 Bx C And Soil K Download Table
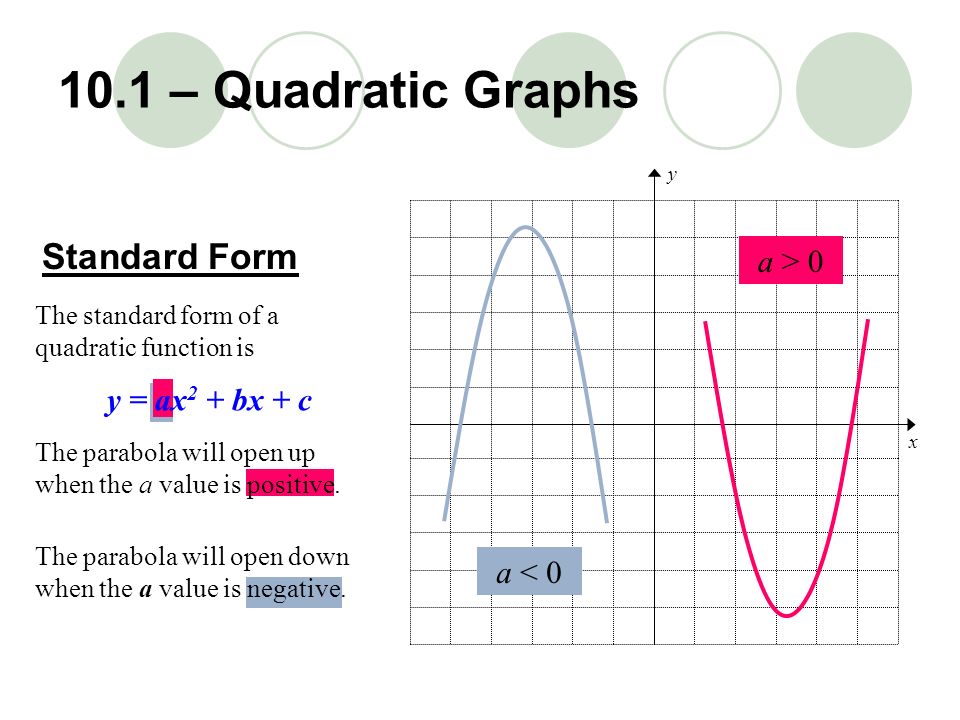



10 1 Quadratic Graphs Ppt Download




9 2 Graphing Y Ax2 Bx C Youtube




Y Ax2 Bx C Quadratic Function Ppt Download



Exploring Parabolas Y Ax 2 Bx C




Ppt Graphing General Quadratics Y Ax 2 Bx C Powerpoint Presentation Id
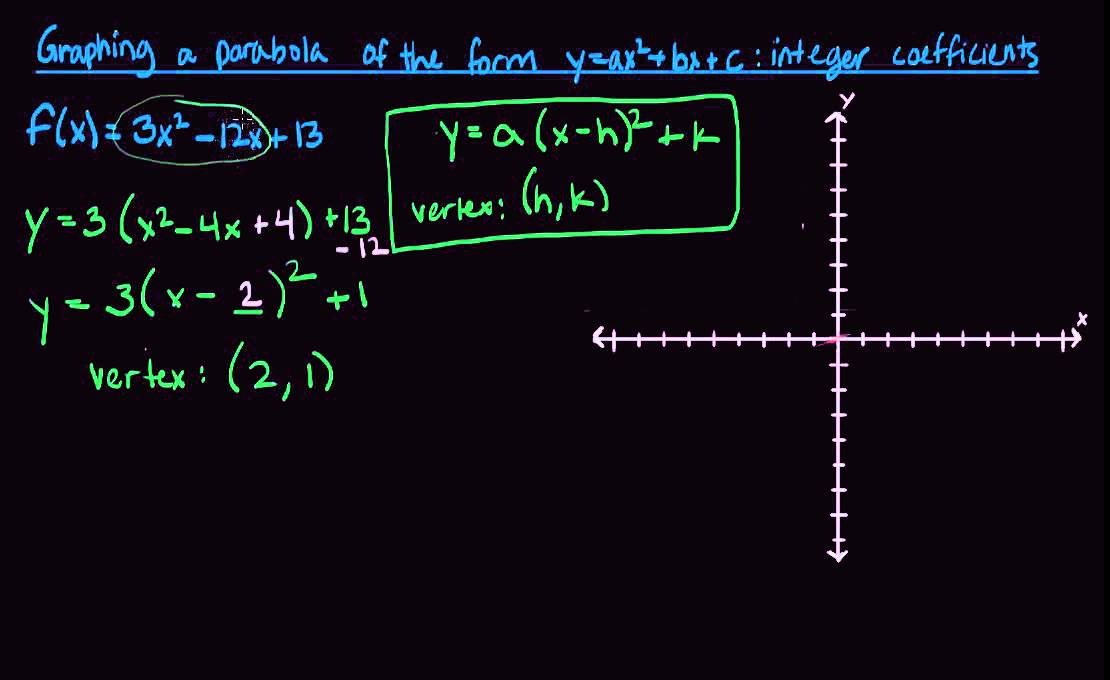



Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
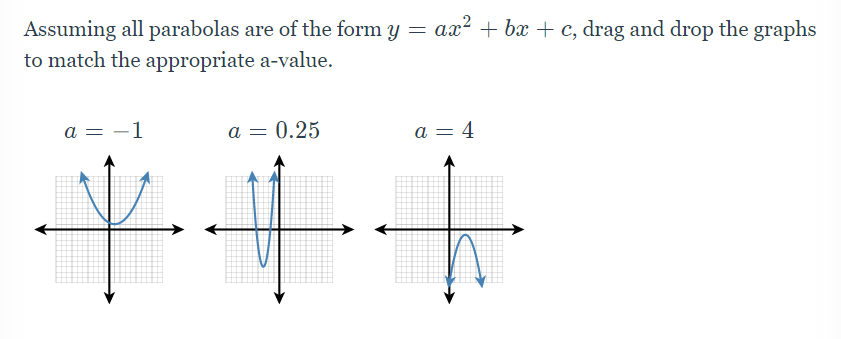



Answered Assuming All Parabolas Are Of The Form Bartleby




Get Answer Show Transcribed Image Text 21 The Curve Y Ax 2 Bx C Shown Transtutors



Search Q Parabola Equation Tbm Isch




Answered 101 Find The Quadratic Function Y Ax2 Bartleby



Graphing Quadratic Functions Of The Form Y Ax 2 Bx C Example 1 Video Algebra Ck 12 Foundation



Determine The Coefficients A B And C Of The Para Gauthmath
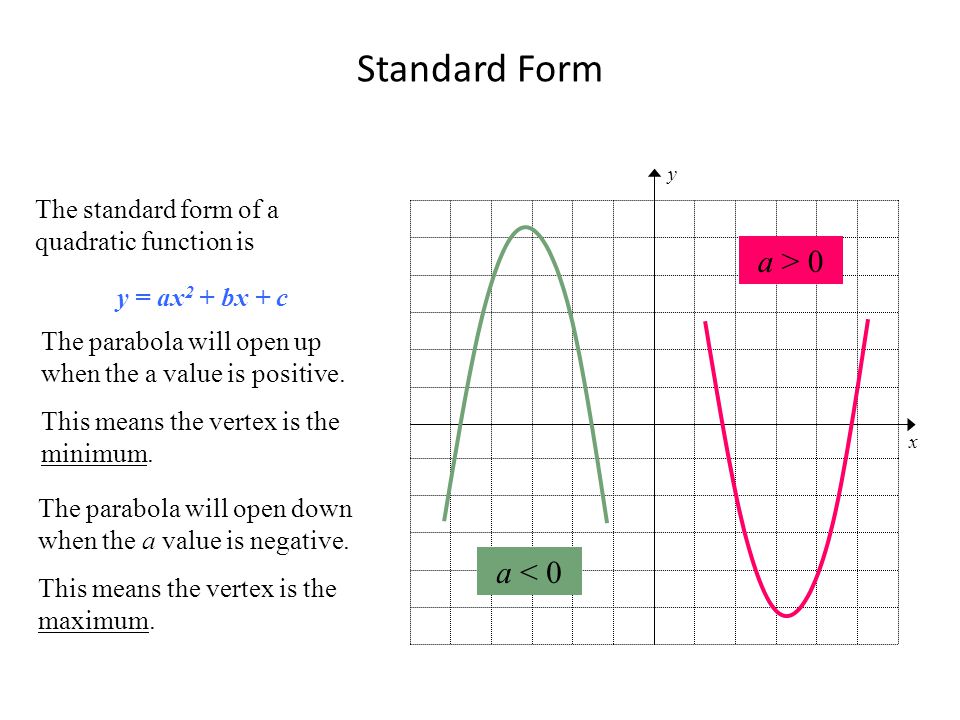



Topic U2 L1 Parts Of A Quadratic Function Graphing Quadratics Y Ax 2 Bx C Eq Can I Identify The Vertex Axis Of Symmetry X And Y Intercepts Ppt Download
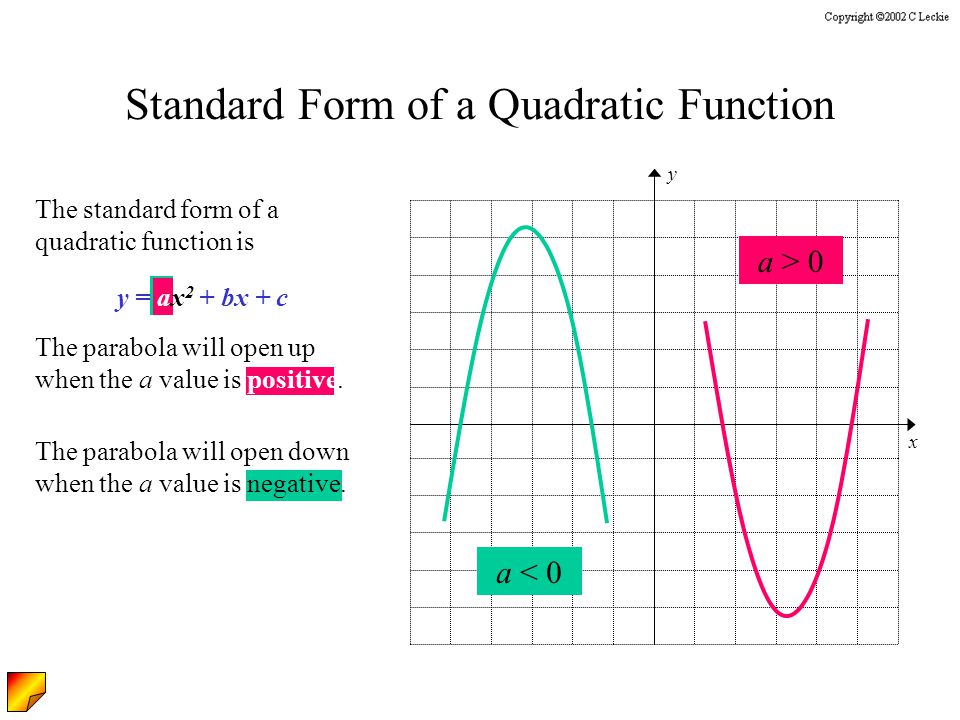



Lesson 10 2 Quadratic Functions And Their Graphs Y Ax 2 Bx C Ppt Download




Graphing Quadratic Functions Y Ax 2 Bx C
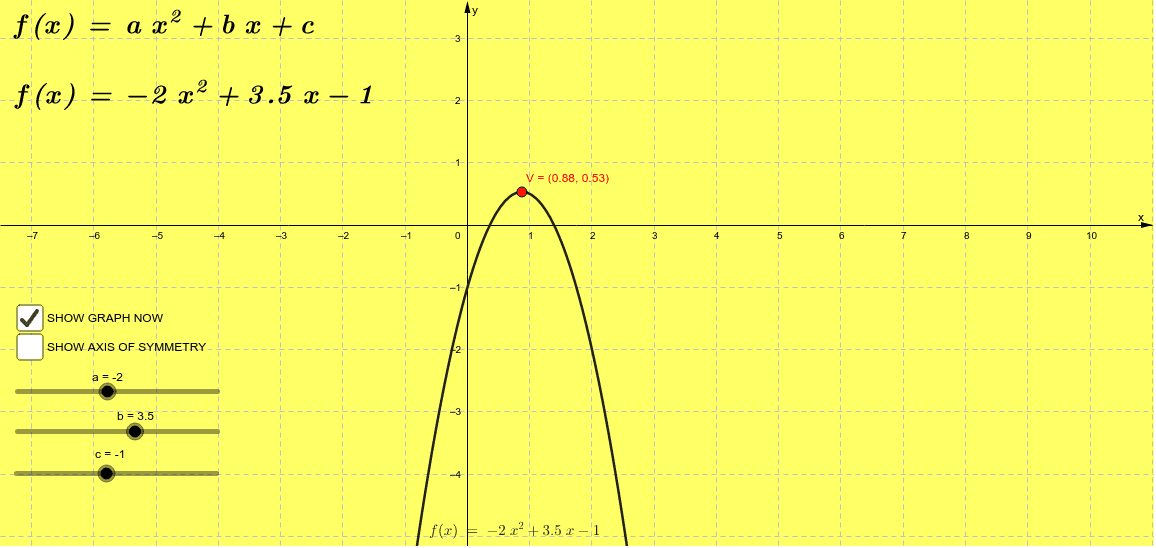



The Quadratic Function Y Ax2 Bx C Geogebra




Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego



Linear Algebra Webnotes Class Assignments Chapter 1




Clockwise Markers For The Functions Linear Y Ax B Quadratic Y Download Scientific Diagram
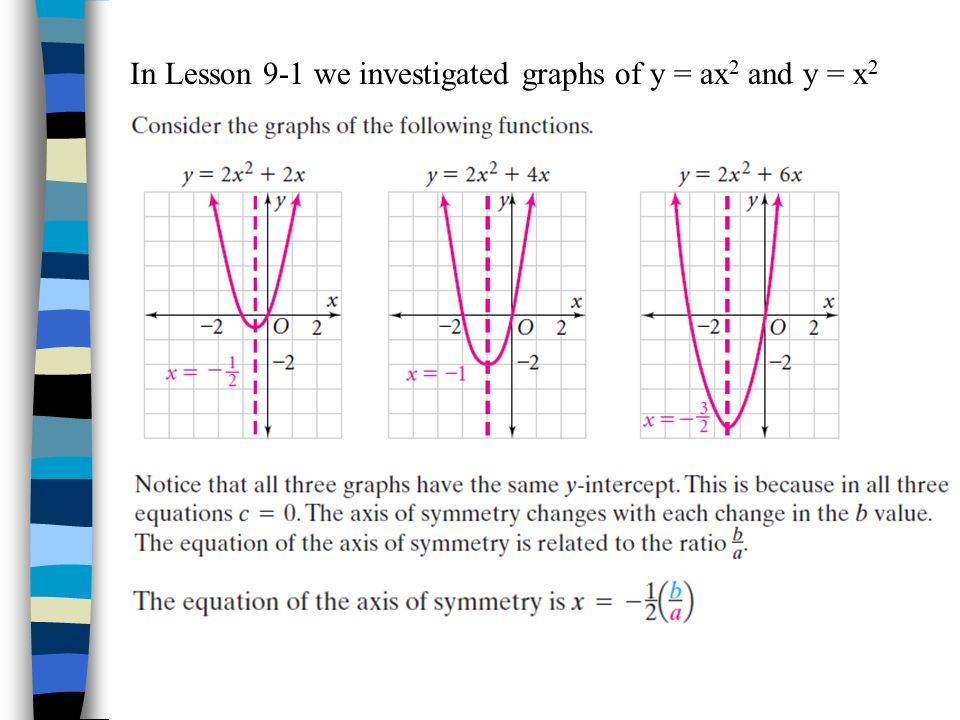



Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download
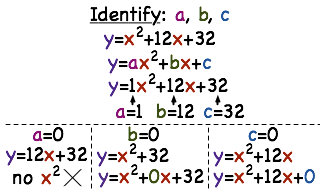



How Do You Find The A B And C Values Of A Quadratic Function Printable Summary Virtual Nerd



Differentiate The Function Y Ax 2 Bx C Youtube



Algebra 1 Activity Sheet Understanding How B Affects The Graph Of Y Ax 2 Bx C




Ppt Expanded Form Y Ax 2 Bx C Powerpoint Presentation Free Download Id 322



Solution Discriminating Quadratics Underground Mathematics



Quadratics
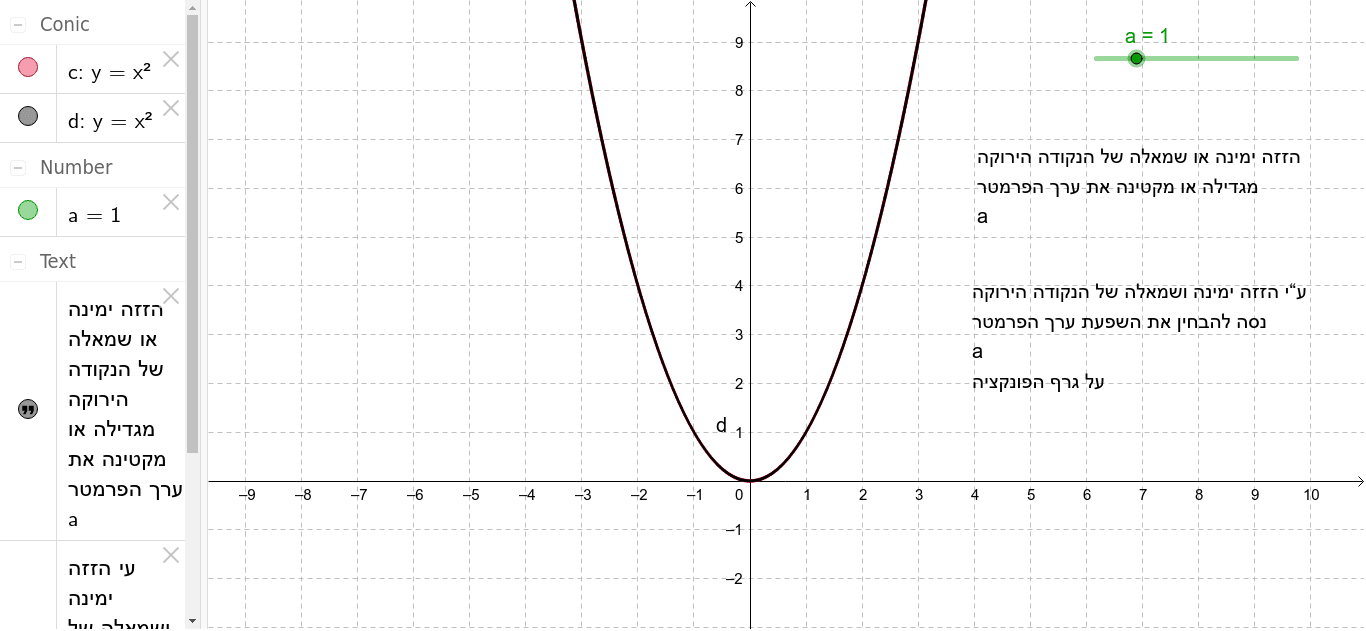



Y Ax 2 Bx C Geogebra




Graphing Y Ax 2 Bx C



Quadratics




Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download
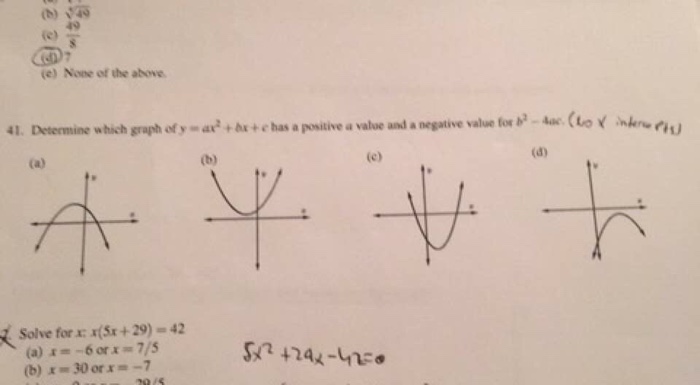



Determine Which Graph Of Y Ax 2 Bx C Has A Chegg Com



How To Show That The Vertex Of The Parabola Math Y Ax 2 Bx C Math Can Be Expressed As Math B 2a C B 2 4a Math Quora
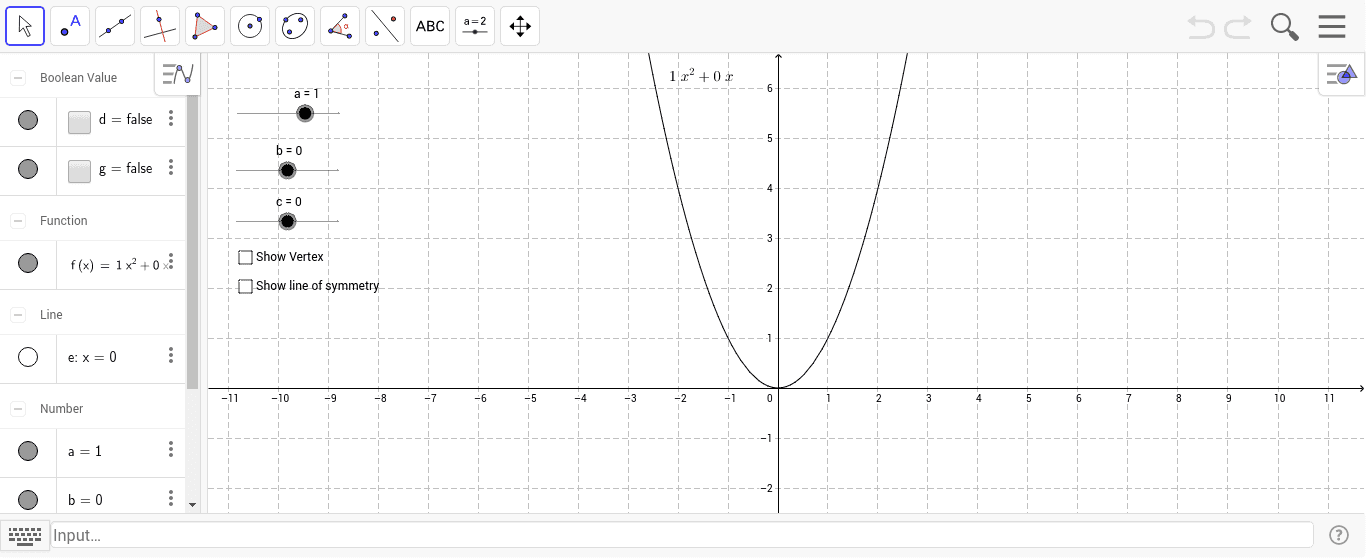



Quadratic In Standard Form Y Ax 2 Bx C Alter The Coef Geogebra



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego
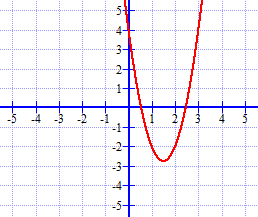



Braingenie Graphing Y Ax Sup 2 Sup Bx C Using A Table Of Values




1 8 Quadratic Functions A Function F Defined By A Quadratic Equation Of The Form Y Ax 2 Bx C Or F X Ax 2 Bx C Where C 0 Is A Quadratic Ppt Download




Finding The Inverse Of Y Ax2 Bx C By Completing The Square Youtube




Factoring Ax2 Bx C



If Ax Bx C 0 And A B C 0 What Would Be The Value S Of X Quora




Review Y Ax2 Bx C Is A Parabola If A 0 The Parabola Is Oriented Upward And The Vertex Is The Minimum Point Of The Function If A 0 The Ppt Download




The Expression Y Ax 2 Bx C Has Always The Same Sign As Of A If A 4ac Lt B 2 B 4ac Youtube




The Graphs Of 17 Given Points Red And Of The Approximate Functions Y Download Scientific Diagram
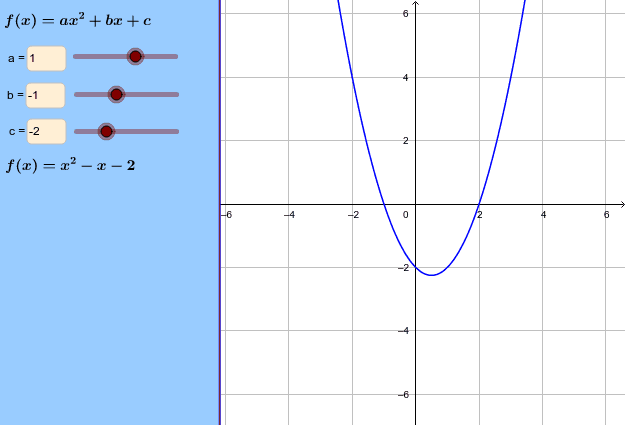



The Graph Of Y Ax 2 Bx C Geogebra




This Is What The Problem Says Assuming All Parabolas Are Of The Form Y Ax 2 Bx C Drag And Drop The Brainly Com




Graphing Y Ax2 Bx C Youtube



Quadratics



1
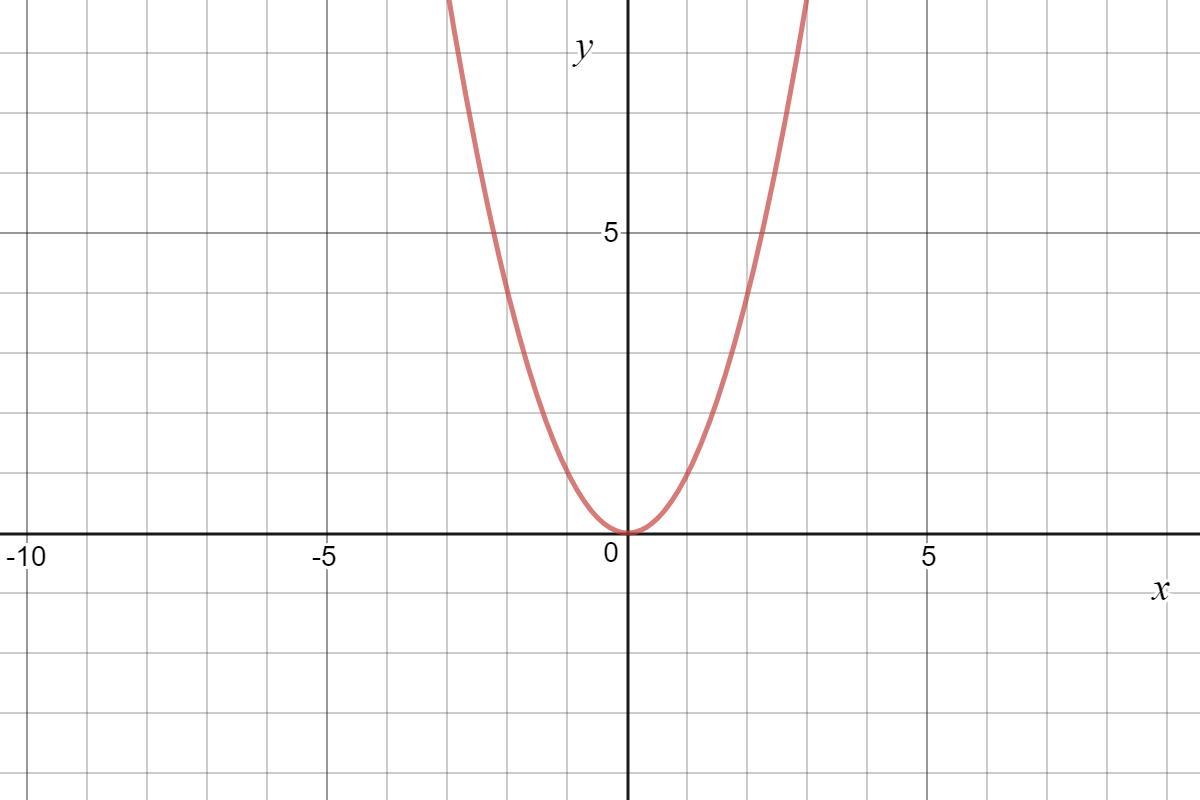



Quadratic Graph Example Y Ax C Expii




Exploring Quadratic Graphs Ppt Video Online Download



0 件のコメント:
コメントを投稿